Recently, the Innovation Academy for Precision Measurement Science and Technology (APM), together with institutions such as Northwest University, the University of Hong Kong, the University of Houston in the United States, and Zhejiang University, has innovatively established an exact solution algorithm system based on "multi-label classification". For the first time, it has achieved a rigorous solution of the spectral function of one-dimensional Bose gases across the entire energy-momentum space under arbitrary interaction strengths, and successfully observed the singular behavior at the spectral boundary. As a result, the research team verified the theoretical predictions of the Nonlinear Luttinger Liquid Theory (NTLL) at the scale of 4,000 particles, providing a new theoretical approach for the study of one-dimensional strongly correlated quantum systems. The relevant research findings were recently published in National Science Review.
Since the discovery of the Mott insulator-metal phase transition, quantum strongly correlated many-body systems have become one of the core research areas in condensed matter physics due to their rich and novel physical phenomena. With the breakthrough advancements in experimental techniques for ultracold atoms, theoretical and experimental research on low-dimensional strongly correlated systems has ushered in a new upsurge. The key to understanding quantum many-body systems lies in the precise characterization of the properties of their correlation functions. However, due to the absence of an effective single-particle picture in strongly correlated systems, traditional perturbative theoretical approaches face fundamental challenges. Against this backdrop, quantum integrable systems with exact analytical solutions have emerged as a crucial approach for understanding the physics of strongly correlated systems.
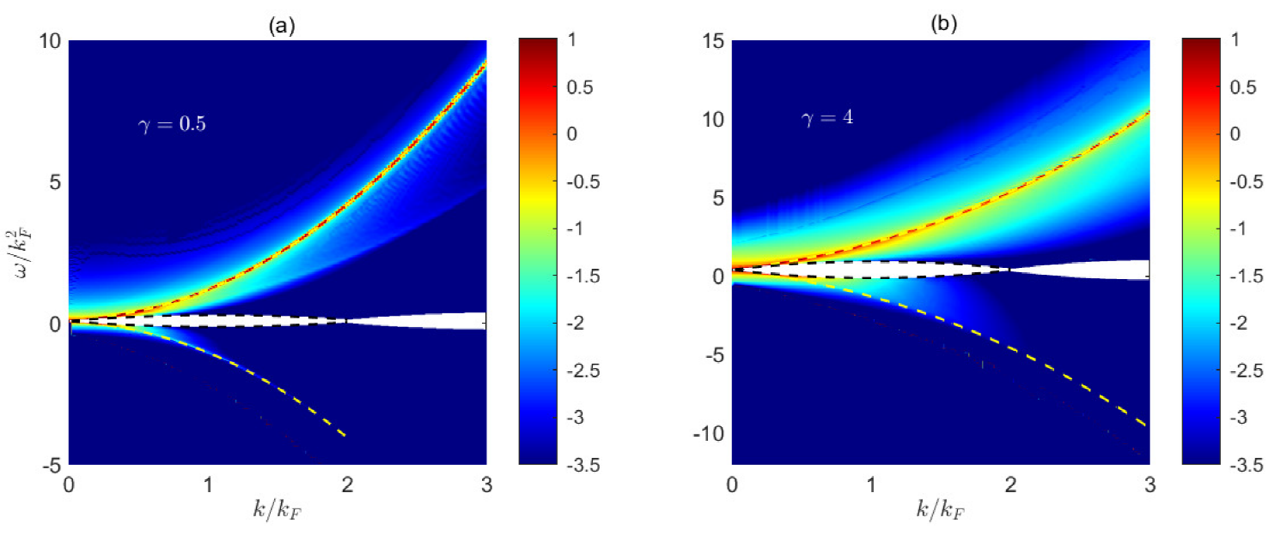
The contour plot of the spectral function in the momentum-energy space shows that higher brightness in color indicates higher spectral weight.
The left figure shows weak interaction (γ = 0.5); the right figure shows moderate interaction (γ = 4.0).
The research team, based on the Bethe ansatz exact solution method, originally proposed the concept of "relative excitation", thereby successfully incorporating the ground state, finite-temperature equilibrium states, and non-equilibrium steady states into a unified processing framework. By introducing four quantum numbers (Pm, Np, Pl, Nl) with clear physical meanings as labels for subspaces of the Hilbert space, the infinite-dimensional Hilbert space is divided into a series of finite-dimensional subspaces, greatly improving computational efficiency. Using this method, the team first precisely calculated the complete spectral function of a one-dimensional Bose gas in the momentum-energy plane, as shown in Figure 1. It is particularly noteworthy that by observing the line shape of the spectral function, a universal power-law behavior of the spectral function at the spectral boundary was successfully obtained for a huge system size of 4,000 particles. This also marks the first confirmation of the natural emergence of the NTLL theory in large-size systems. As shown by the fitting results in Figure 2, the four critical exponents (-0.465, 1.141, -0.529, 0.977) are in highly good agreement with the predictions of the NTLL (-0.422, 0.934, -0.501, 1.043)! This is the first time in the research of quantum integrable models that the theoretical predictions of the NTLL have been clearly observed and quantitatively confirmed. In addition, the research team also calculated the momentum distribution function of a one-dimensional Bose gas and observed the power-law behaviors of the linear TLL theory and Tan’s Contact in the low-momentum and high-momentum regions respectively, as shown in Figure 3.
The research achievements on the precise spectral function of one-dimensional Bose gases this time have provided direct support for recent experimental observations of one-dimensional Luttinger liquids, injected new vitality into the study of quantum many-body systems, and offered new perspectives for future ultracold atom experiments as well as the exploration of quantum technologies based on quantum many-body physics.
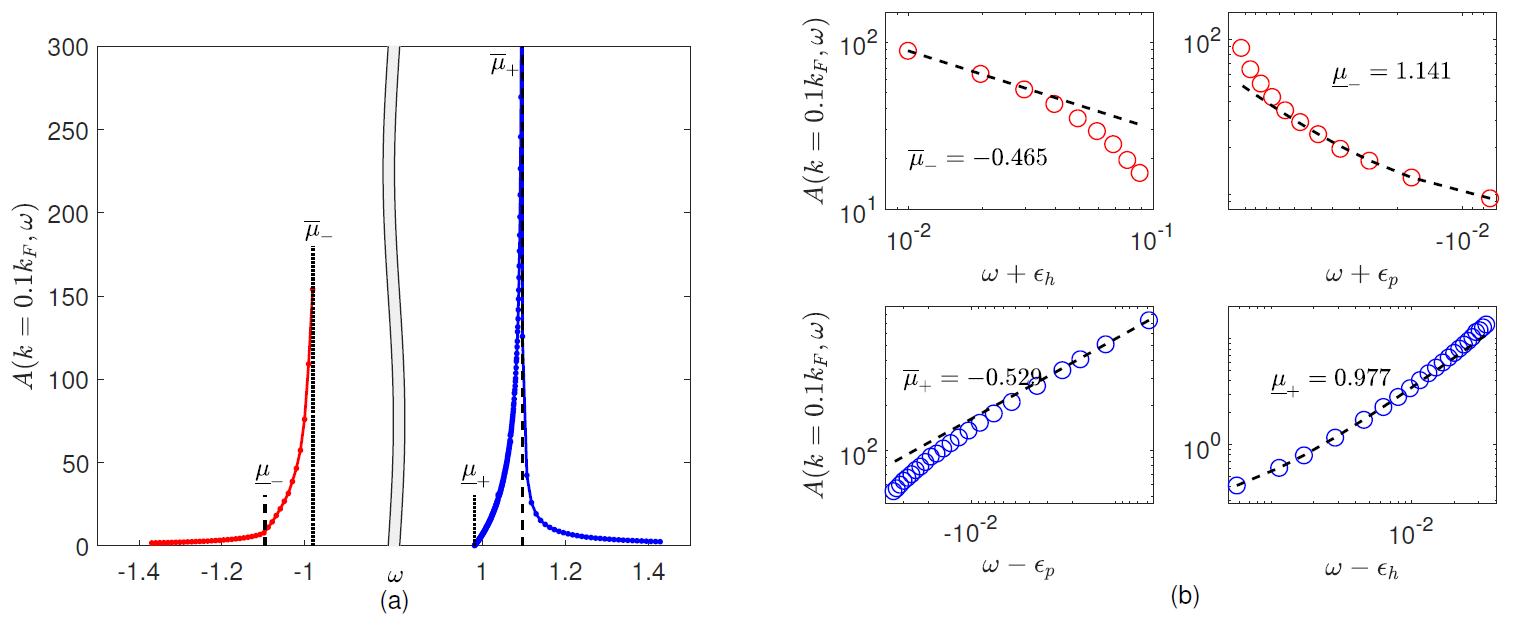
(a) The curve depicting how the spectral function at k=0.1kF varies with energy under moderate intensity (γ=4.0). The black dashed line and dotted line mark the boundaries of Type I and Type II excitation spectra, respectively.
(b) The power-law behavior of the spectral function near the four boundaries. The red and blue circles represent the calculated results, while the black dashed line indicates the fitted power-law curve.
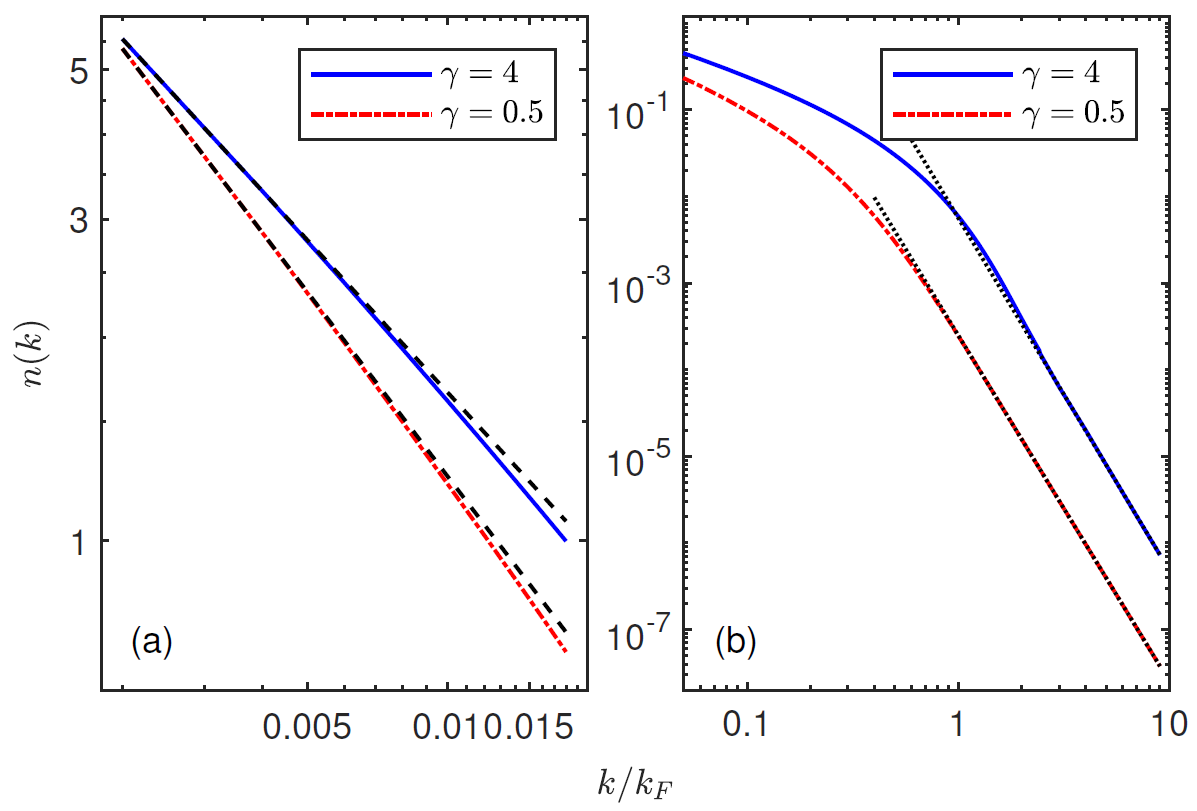
(a) In the low-momentum region, n(k)∝kα. The black dashed lines show the fitted slopes α as −0.750 (γ=4.0) and −0.908 (γ=0.5), which are in accordance with the predictions of −0.737 and −0.894 from the linear Luttinger liquid theory.
(b) In the high-momentum region, n(k)∝k−4. The black dashed lines display the fitted slopes as −4.073 (γ=4.0) and −4.001 (γ=0.5), perfectly consistent with the universal law of contact-interaction systems, namely, Tan’s Contact.
The relevant research findings were published in the journal National Science Review under the title "Exact spectral function of one-dimensional Bose gases". Dr. CHENG Song, a research assistant at the University of Hong Kong, and Associate Professor CHEN Yangyang from Northwest University are the co-first authors (both are doctoral graduates from APM). CHEN Yangyang, GUAN Xiwen, and Professor LIN Haiqing from Zhejiang University are the co-corresponding authors. Other co-authors include Professor YANG Wenli from Northwest University and Professor RUBEM Mondaini from the University of Houston in the U.S.
This research has received funding and support from multiple institutions, including the National Natural Science Foundation of China, the Hong Kong Research Grants Council, and the Chinese Academy of Sciences.
Link to the article: https://academic.oup.com/nsr/article/12/9/nwaf294/8209836
